


NOTE: the symbol "V" is sometimes used to represent voltage instead of "E". In some cases, an author or circuit designer may choose to exclusively use "V" for voltage, never using the symbol "E." Other times the two symbols are used interchangeably, or "E" is used to represent voltage from a power source while "V" is used to represent voltage across a load (voltage "drop").
"The algebraic sum of all voltages in a loop must equal zero."
Kirchhoff's Voltage Law (KVL)
"The algebraic sum of all currents entering and exiting a node must equal zero."
Kirchhoff's Current Law (KCL)




Time constant in seconds = RC
Time constant in seconds = L/R


ZL = R + jXL
ZC = R - jXC

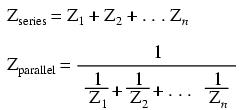
NOTE: All impedances must be calculated in complex number form for these equations to work.
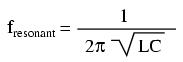
NOTE: This equation applies to a non-resistive LC circuit. In circuits containing resistance as well as inductance and capacitance, this equation applies only to series configurations and to parallel configurations where R is very small.

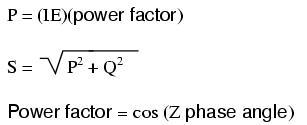

Conversion equivalencies for volume
1 gallon (gal) = 231 cubic inches (in3) = 4 quarts (qt) = 8 pints (pt) = 128 fluid ounces (fl. oz.) = 3.7854 liters (l)
Conversion equivalencies for distance
1 inch (in) = 2.54 centimeter (cm)
Conversion equivalencies for weight
1 pound (lb) = 16 ounces (oz) = 0.45359 kilogram (kg)
Conversion equivalencies for area
1 acre = 43560 square feet (ft2) = 4840 square yards (yd2)
Conversion equivalencies for pressure
1 pound per square inch (psi) = 2.03602 inches of mercury (in. Hg) = 27.6799 inches of water (in. W.C.) = 6894.76 pascals (P) = 0.068046 atmospheres (Atm) = 0.068948 bars
Conversion equivalencies for energy or work
1 british thermal unit (BTU) = 251.996 calories (cal) = 1055.056 joules (J) = 0.293071 watt-hour (W-hr)
Conversion equivalencies for power
1 horsepower (hp) = 745.7 watts (W) = 2544.43 british thermal units per hour (BTU/hr)
Converting between units is easy if you have a set of equivalencies to work with. Suppose we wanted to convert an energy quantity of 2500 calories into watt-hours. What we would need to do is find a set of equivalent figures for those units. In our reference here, we see that 251.996 calories is physically equal to 0.293071 watt hour. To convert from calories into watt-hours, we must form a "unity fraction" with these physically equal figures (a fraction composed of different figures and different units, the numerator and denominator being physically equal to one another), placing the desired unit in the numerator and the initial unit in the denominator, and then multiply our initial value of calories by that fraction.
Since both terms of the "unity fraction" are physically equal to one another, the fraction as a whole has a physical value of 1, and so does not change the true value of any figure when multiplied by it. When units are canceled, however, there will be a change in units. For example, 2500 calories multiplied by the unity fraction of (0.293071 w-hr / 251.996 cal) = 2.9075 watt-hours.

The "unity fraction" approach to unit conversion may be extended beyond single steps. Suppose we wanted to convert a fluid flow measurement of 175 gallons per hour into liters per day. We have two units to convert here: gallons into liters, and hours into days. Remember that the word "per" in mathematics means "divided by," so our initial figure of 175 gallons per hour means 175 gallons divided by hours. Expressing our original figure as such a fraction, we multiply it by the necessary unity fractions to convert gallons to liters (3.7854 liters = 1 gallon), and hours to days (1 day = 24 hours). The units must be arranged in the unity fraction in such a way that undesired units cancel each other out above and below fraction bars. For this problem it means using a gallons-to-liters unity fraction of (3.7854 liters / 1 gallon) and a hours-to-days unity fraction of (24 hours / 1 day):
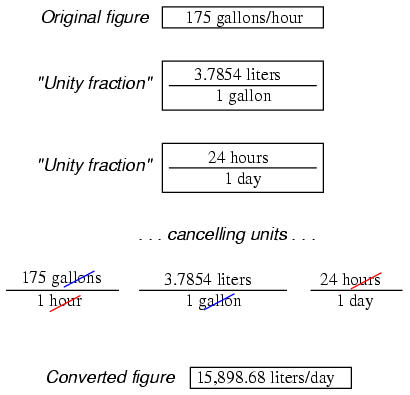
Our final (converted) answer is 15898.68 liters per day.


